Quanto distano le stazioni ferroviarie di San Candido, borgo della provincia di Bolzano a pochi passi dal confine austriaco, e Calalzo, comune nella valle del Cadore, non lontano da Cortina d’Ampezzo? Un rapido sguardo a una carta geografica ci suggerisce che sono piuttosto vicine: in linea d’aria tra i due comuni ci sono circa 30 km, distanza che un treno regionale può coprire in una ventina di minuti. Tuttavia, se provate ad acquistare un treno da Calalzo a San Candido, la soluzione più veloce prevederà cambi a Ponte Nelle Alpi, poi Venezia, quindi Verona e infine Fortezza: totale, 4 coincidenze, 8 ore e 42 minuti di viaggio. Anche tenendo conto che le due località sono separate da una regione montana, resta il fatto che un ciclista anche non allenato ci metterebbe decisamente meno tempo in bicicletta.

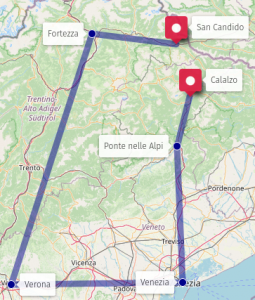
Ovviamente c’è una spiegazione banale per questa discrepanza: la rete ferroviaria italiana non prevede un collegamento diretto tra Calalzo e San Candido – e neppure tra Calalzo e Venezia, o Venezia e San Candido; e nel momento in cui dobbiamo fare un viaggio in treno, è appunto la rete ferroviaria che ci interessa – l’effettiva distanza geografica tra i luoghi è di per sé irrilevante.

Distanze non geografiche

Sono molte le situazioni in cui tra due luoghi, persone o entità di altro tipo ci interessa identificare una distanza che però non è quella geografica. Anzi: spesso ci interessa misurare la distanza tra cose che non hanno neanche una loro collocazione geografica: due profili Facebook, due articoli scientifici, due settori industriali. In tutti questi casi – e in moltissimi altri – la distanza che vogliamo esprimere è, come nel caso delle stazioni ferroviarie, da cercare in una determinata rete. Ed è di questo che si occupa la teoria delle reti, di situazioni in cui all’interno di un gruppo di cose – che in gergo chiamiamo nodi – possono esistere o meno  connessioni che chiamiamo archi. Nel nostro esempio, nella rete ferroviaria c’è un arco tra Calalzo e Ponte Nelle Alpi, ma non tra Calalzo e San Candido; e similmente, nella rete di Facebook c’è un collegamento tra due account solo se sono amici, e nella rete di citazioni scientifiche c’è un collegamento tra due articoli solo se uno cita l’altro.

Il problema dei sette ponti

Ciò che nelle scienze sociali chiamiamo “rete” (in inglese, network) – appunto, nodi collegati da archi – coincide con quello che i matematici studiano, chiamandolo invece “grafo”, da decenni, anzi da secoli. Fu il matematico svizzero Eulero, infatti, che si pose l’obiettivo di risolvere un problema all’apparenza banale: se fosse possibile, nella oggi russa e al tempo prussiana città di Königsberg (Kaliningrad), fare una passeggiata che attraversasse una e una sola volta ognuno dei suoi sette ponti.

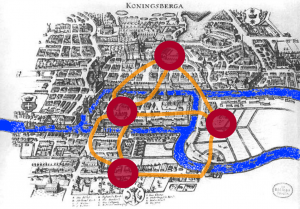
Eulero dimostrò che era impossibile, e nella sua dimostrazione non assunse alcun ruolo la lunghezza dei ponti o lo spazio che li separa: tutto ciò che conta è che ogni ponte rappresenta una connessione tra due parti di città – un arco tra due nodi. Siccome ogni volta che si passa da un nodo si percorre due ponti (uno entrando e uno uscendo), se un nodo ha un numero dispari di ponti bisognerà, per percorrerne ognuno una sola volta, o partire da quel nodo o terminarci il percorso. Ma siccome nella Königsberg dell’epoca ognuna delle parti della città era servita da un numero dispari di ponti, il percorso avrebbe dovuto avere in ognuna delle quattro parti o il suo inizio o la sua fine, il che è chiaramente impossibile. Era il 1736 e questo fu il primo risultato della teoria dei grafi. Per la cronaca, in gergo oggi riassumeremmo questo risultato dicendo che il grafo in questione è non euleriano, dal nome ovviamente del grande matematico.

I metri non contano

In ogni rete possiamo parlare di “distanza” tra due nodi senza ricorrere a metri o chilometri, ma di passaggi necessari per andare da un nodo a un altro. Per esempio, nella città di Königsberg, due parti collegate da un ponte sono a distanza 1; ma si può osservare che le due parti raffigurate in basso e in alto non sono collegate da un ponte. Per andare dall’una all’altra bisogna passare per esempio dall’isola centrale, percorrendo due ponti: la loro distanza non è quindi 1 ma 2.

Percorsi “pesati”

Ai cittadini di Königsberg che volevano passeggiare attraverso ogni ponte non importava se uno di questi fosse più o meno lungo. Ma in altre reti non tutti gli archi sono equivalenti, e di questo è importante tenere conto. Per esempio, nella rete ferroviaria ci saranno archi – come quello tra Calalzo e Ponte nelle Alpi – più brevi e altri – come quello tra Verona e Fortezza – più lunghi: ovviamente questa osservazione ha un’importanza cruciale se vogliamo trovare la strada più breve possibile tra due stazioni. Consideriamo quindi la rete ferroviaria un network pesato, nel senso che a ogni arco assegniamo un peso che potrà essere la sua lunghezza in chilometri se vogliamo trovare la soluzione che ci fa percorrere meno strada, oppure la sua durata in minuti se vogliamo trovare la soluzione più breve, o ancora il suo costo in euro se vogliamo pagare il meno possibile.

Reti lunghe o compatte

Le distanze tra nodi di una rete – che siano pesate, come nel caso della rete ferroviaria, o meno, come nel caso dei ponti di Königsberg – sono cruciali non solo per trovare il percorso più breve tra due nodi, ma anche per farci un’idea di come sia fatta la rete nel suo complesso, e per capire alcuni fenomeni che si svolgono sulla rete. Ci saranno reti molto “allungate”, con coppie di nodi lontani tra di loro – è questo il caso di molecole organiche come il DNA, se consideriamo nodi gli atomi e archi i legami chimici tra di essi – e reti più “compatte”, in cui tutti i nodi sono relativamente vicini tra di loro. Tendono a ricadere in questo secondo gruppo la maggior parte delle reti sociali, di cui ci occuperemo nella prossima puntata.

Link e approfondimenti

• Il libro La responsabilità di rete (il Mulino) di Pietro Battiston, e il suo sito.