I numerosi articoli apparsi su Josway che parlano di ragnatele, ci obbligano a suggerire una loro esplorazione con lo sguardo matematico. Dobbiamo però evitare di impigliarci subito, come nella drammatica canzone della tartaruga e del reggilattine, anche se il rischio è alto. Sin dalla mattina, ascoltando il ribollire del vapore mentre percola attraverso lo strato di caffè della nostra moka, mentre scorriamo velocemente le risposte ricevute ai messaggi sui social network, per andare prima al sito che riporta gli ultimi dati sulla pandemia, non facciamo altro che districarci in una moltitudine di reti: quella dei percorsi del vapore tra le particelle di caffè, quelle sociali dei pettegolezzi, quella del contagio. E a nulla vale cercare di sfuggire, posando per un istante lo sguardo sulla foglia caduta sul terrazzo dal pioppo in giardino: i diagrammi di Voronoi delle sue venature ci richiamano alla mente la cyber-analisi del gol subito dalla nostra squadra nell’ultima partita. Non sembra più possibile riflettere sul mondo, senza fare i conti con la teoria delle reti. Ma come abbiamo potuto farne a meno prima d’ora?

Avrei voluto offrire un’agile guida alla sopravvivenza in rete, ma solo con questa breve introduzione ci siamo già terribilmente invischiati con i link, nella foresta incantata del World Wide Web, che è l’universo immateriale, o se mi si concede nuvoloso, nel quale crescono le ragnatele tessute dai nostri avatar. Non ci rimane che il gioco… matematico, si intende, per prendere con filosofia quest’ossessione e sciogliere qualche incantesimo.

Nodi, archi e grafi

Il concetto matematico di rete è il grafo. Un grafo costituito da nodi ed archi: gli incroci tra venature nella foglia di pioppo sono i nodi (o vertici), i tratti tra due nodi sono gli archi.

Problema 1: i ponti di Königsberg

Due sono i problemi famosi sui grafi. Il primo è noto come il Problema dei ponti di Königsberg, che si può formulare così: “Nella sua salutare passeggiata quotidiana, il filosofo Immanuel Kant può attraversare tutti i ponti della città una e una sola volta, prima di rientrare a casa?”. L’amico Eulero spiegò a Kant come ciò non sia possibile, perché tutti e quattro i rioni di Königsberg hanno un numero dispari di ponti. Se si inizia il percorso in un rione qualsiasi, non lo si può terminare nello stesso rione, perché i ponti che imbocchiamo in uscita devono essere tanti quanti quelli che imbocchiamo in entrata. Dunque non c’è un circuito chiuso che attraversi tutti i ponti una e una sola volta.

Problema 2: i colori delle regioni

L’altro problema riguarda la colorazione delle mappe: “Qual è il minimo numero di colori con i quali si possono tingere le regioni italiane in una cartina, senza che ci siano due regioni confinanti con lo stesso colore?”. Per “confinanti” intendiamo due regioni che si toccano per un tratto non costituito da un solo punto. Questo per mettere i proverbiali puntini sulle “i”, e i proverbiali (in inglese) taglietti sulle “t”. Per colpa dell’Umbria, sono necessari 4 colori, infatti la Toscana confina sia con il Lazio che con le Marche, e le Marche confinano con il Lazio. Ebbene, il fatto sorprendente è che bastano 4 colori, qualunque sia la frammentazione delle zone. Bastano 4 colori anche per colorare gli oltre ottomila comuni d’Italia, senza che due comuni confinanti abbiano lo stesso colore! Incidentalmente, faccio notare che la dimostrazione del fatto che bastano sempre solamente 4 colori è stato un problema aperto per molto tempo, e quando fu chiuso nella dimostrazione si fece un uso massiccio del computer per controllare un gran numero di casi. Ciò mise in crisi il concetto stesso di dimostrazione.

Una regola universale

Voglio infine ricordare un’ulteriore proprietà, detta caratteristica di Eulero, che vale per tutte le reti piane, per quanto possano sembrare complesse.

Considerate la foglia di pioppo, è facile distinguere vertici, archi e regioni. I vertici – lo ricordiamo – sono gli incroci tra due venature. Gli archi sono i tratti di venature tra due incroci e le regioni sono le aree di foglia senza venature. Se considerate l’esterno della foglia come una regione, allora il numero delle regioni più quello degli spigoli è uguale a quello dei vertici più due: R+S=V+2. Sorpresi? Provate a verificarlo disegnando alcune reti a caso su un foglio.

Reti sociali

Oggigiorno, però, c’è una nuova specie di rete molto invasiva nella nostra quotidianità, la rete sociale. Nelle reti sociali, gli individui sono i nodi e un legame di amicizia tra due individui rappresenta un arco. La loro evoluzione è affascinante, poiché avvengono alcuni cambiamenti di fase come in chimica. Fino a quando la media degli amici di un nodo è minore di 1, il grafo è costituito da numerose componenti connesse di piccole dimensioni; ma, quando il numero medio di amici è superiore a 1, allora di solito compare un’unica componente connessa gigante. Adesso però non fatevi venire l’ansia se appartenete alla componente gigante della vostra rete sociale preferita.

I ricchi con i ricchi

Le reti sociali sono assortative, ovvero i nodi con tanti amici tendono a collegarsi agli altri che hanno tanti amici. Questa dinamica purtroppo induce all’emarginazione e alle disparità: i ricchi tendono a frequentare ricchi, i famosi i famosi. Non tutte le reti sono assortative, però. Per esempio, i collegamenti aerei non lo sono: le compagnie tendono a collegare gli hub con scali minori per assicurarsene il monopolio e ottenere così collegamenti più redditizi.

Sei gradi di parentela

Un’altra caratteristica sorprendente delle reti sociali è la cosiddetta Teoria del mondo piccolo, secondo la quale prendendo a caso due vertici c’è sempre un cammino abbastanza breve che li collega. È la teoria dei 6 gradi di parentela avanzata dallo psicologo sociale Stanley Milgram negli anni ’60. Comunque si prendano due persone al mondo, queste sono collegate da un cammino di conoscenze che ha al più una decina di nodi. Questo pensiero ci porta agli iperconnettori, ovvero agli super-spreader delle pandemie di Covid-19 e Aids. Provate a stabilire una catena che vi colleghi a me attraverso delle persone che si sono strette la mano almeno una volta nella loro vita.

Amicizia e paradossi

Ma ancora più sconvolgente è il paradosso dell’amicizia, il cui insegnamento mi sembra importante anche sul piano psicologico: “È vero che, in una rete sociale in media, ho molti più amici dei miei amici?”. Molti ne sono convinti, ma ahimè si illudono. La verità è amara: in una rete sociale è vero l’opposto, e in media i miei amici hanno più amici di me. Tutto discende dal fatto, quasi ovvio, che è molto più facile essere connessi con nodi che hanno un alto numero di contatti, gli hub o super-spreader, piuttosto che con nodi isolati. In una rete sociale, la media del numero degli amici di un amico di una persona generica è maggiore della media dei suoi amici. Questo tipo di fenomeno, che si applica anche a reti non simmetriche, come quella dei follower, e a misure diverse come il numero di contenuti virali o la mole di attività, non deve però avvilirci troppo. Da un lato il risultato è dato in media; ma soprattutto, come dice il proverbio, mal comune mezzo gaudio.

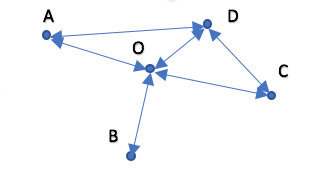
Il calcolo delle medie

La giustificazione matematica di questa proprietà dipende da come calcoliamo le medie. Chi volesse può provare a fare il conto su un grafo disegnato a caso. In quello tracciato in figura, per esempio, la media degli amici di un nodo è pari a  (2+1+2+3+4)/5=12/5=2,4. Mentre la media degli amici degli amici di un nodo è maggiore: ((4+3)/2+4/1+(4+3)/2+(2+4+2)/3+(2+1+2+3)/4)/5=3,1. E anche se usassimo la media pesata degli amici degli amici otterremmo un valore maggiore. Infatti in questa rete si vede facilmente che i nodi hanno in maggioranza meno amici della media dei loro amici (vale per A, B e C). Questo fatto non è vero in generale, anche se si verifica nelle reti sociali che hanno ampie variabilità tra il numero di collegamenti. Il punto è che la popolarità dipende da come la si conta, e non va mai confusa con la vera amicizia.

Automi cellulari: il gioco della vita

Chiudiamo con un ultimo tipo di rete: un automa cellulare è costituito da un network di cellule, ciascuna collegata a un certo numero di cellule vicine. Ogni cellula si trova in uno stato, tra un numero finito di stati possibili, che può mutare ad ogni tic dell’orologio a seconda degli stati delle cellule vicine. L’automa cellulare più famoso è il gioco della vita del matematico inglese John Conway. La rete è una scacchiera di dimensioni qualsiasi e le cellule sono le caselle. Ogni casella è vicina a 8 caselle, perché si considerano vicine anche quelle in diagonale. Ogni casella può essere viva o morta. La dura legge della vita è la seguente: una casella viva con meno di 2 caselle vive vicine muore d’isolamento; una casella viva con 2 o 3 caselle vive vicine sopravvive alla generazione successiva; una casella viva con più di 3 caselle vive vicine muore per sovrappopolazione; una casella morta con esattamente 3 caselle vive vicine diventa una casella viva, ovvero nasce. Partendo da una configurazione qualsiasi di caselle vive, l’evoluzione della scacchiera, al succedersi delle generazioni, manifesta complessità sorprendenti. Di fatto, l’automa di Conway può simulare tute le evoluzioni possibili di un sistema complesso, compresa – se crediamo nel meccanicismo – la dinamica della mente umana.