Ci sono numeri che sfuggono a ogni ragionevole comprensione umana, e il numero di Graham è uno di questi. Perfino i matematici lo definiscono “mostruoso”. Ben più del più noto googol, cioè 10100, che abbiamo visto già nella prima puntata di questa serie. Ma il numero di Graham, a sua volta, impallidisce di fronte al suo successore, un numero che è stato scoperto soltanto diversi anni più tardi e che costituisce la terza tappa di questo nostro viaggio nei numeri enormi.
Tappa 3. TREE(3)
Così come il numero di Graham, TREE(3) non viene vuori dal nulla, solo per il piacere di battere un record. Questo numero emerge infatti da un problema matematico reale, o meglio da un gioco, il “gioco degli alberi”. Immaginiamo di costruire una foresta di alberi a partire da diverse combinazioni di semi. Alberi e semi hanno qui un preciso significato matematico. I semi si possono rappresentare con punti colorati, e diverse tipologie di semi hanno colori diversi. Gli alberi sono costituiti da semi collegati tra loro da linee dette rami. Quando si costruisce una foresta, il primo albero deve avere al massimo un seme, il secondo deve avere al massimo due semi e così via. Non è consentito costruire un albero che “contiene” nella sua struttura uno degli alberi più vecchi, in un senso che si può dettagliare matematicamente, ma che è molto vicino all’idea intuitiva che ci si può fare.
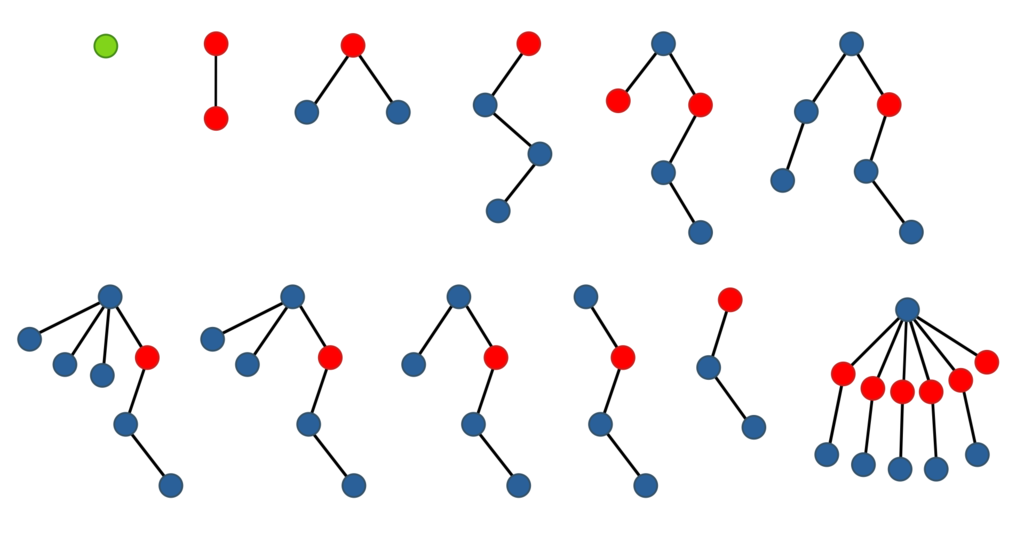
In sequenza
Il problema è allora: quanti alberi si possono costruire in questo modo? La risposta dipende dal numero di diverse tipologie di semi a disposizione, cioè dei colori disponibili.
Se c’è un solo colore, c’è un solo tipo di albero. Cioè, TREE(1)=1.
Se ci sono due colori, le possibilità sono tre. TREE(2)=3.
Se ci sono tre colori, la foresta esplode. E il numero di alberi diventa mostruosamente grande, pur restando finito. TREE(3)=… un numero grande, grande, grande. Quanto grande? Immaginiamo, ancora una volta, di disegnare un albero nel tempo più breve possibile. Questo tempo si chiama “tempo di Planck”, ed è pari a circa 0,0000000000000000000000000000000000000000001 secondi. In fisica, un tempo inferiore non può esistere, nemmeno in linea di principio. E noi esseri umani siamo ancora molto lontani dall’avere accesso a un tempo così breve. Immaginando però di riuscire a disegnare un albero in un tempo di Planck, dopo un anno ne avremmo molti miliardi di miliardi di miliardi… non vale la pena nemmeno contarli tutti, perché questo numero sarebbe comunque enormemente più piccolo di TREE(3). E se anche andassimo avanti per tutta l’età della Terra, o quella del Sole, o pefino quella dell’universo, ancora non saremmo nemmeno a metà strada. Anzi, non saremmo nemmeno all’inizio. Si pensa che il nostro universo, prima o poi, scomparirà, forse per generarne un altro. Ci vorrà ancora molto, ma molto tempo. Qualunque sia l’età massima possibile per l’universo, però, verosimilmente non basterebbe per contare tutte le possibili configurazioni di TREE(3) e nemmeno del numero di Graham, che pure è molto più piccolo. Il numero di Graham, rispetto a TREE(3), è praticamente zero.
Oltre TREE(3)
Ovviamente, oltre TREE(3) ci sono TREE(4), TREE(5) e così via, fino a TREE(Graham) e oltre. È facile scriverli, praticamente impossibile immaginarli, dato che questa serie cresce più velocemente di qualsiasi altra facilmente concepibile. Ma se si escludono questi numeri ottenuti dall’applicazione di una regola precedente è possibile andare oltre TREE(3)? La risposta è nella prossima puntata
Link e approfondimenti
• La prima puntata della serie sui grandi numeri.
• La crescita esponenziale descritta da Dante Alighieri.
• Googol e googolplex in un video di Numberphile.
• Il numero di Graham spiegato da Ron Graham!
• Un video di Numberphile che spiega in modo chiaro ed efficace che cos’è TREE(3) e quanto è enorme. Poiché si tratta di un numero così grande, c’è pure un video aggiuntivo di extra footage. E il confronto con il numero di Graham.
• Il teorema di Kruskal che dà origine a TREE(3).



