L’universo, si sa, è nato 13,8 miliardi di anni fa, con una grande esplosione detta Big Bang. Giusto? Ni. Perché il Big Bang ci fu, questo è sicuro. Però – a parte chiarire che cosa si intende con “grande esplosione” (cosa semplice, ma che non faremo qui) – l’universo non è propriamente nato con il Big Bang: c’era qualcosa prima. A scommetterci è Gabriele Veneziano, fisico teorico al Collège de France e al Cern di Ginevra, noto per aver avuto nel 1968 un’intuizione – passata alla storia come Ampiezza di Veneziano e celebrata anche dall’artista Anselm Kiefer – che ha portato alla nascita della moderna teoria delle stringhe. Veneziano lavora dagli anni ’90 a un modello cosmologico basato appunto sulla teoria delle stringhe, che consenta di dare ragione del Big Bang e del nostro universo. Lo abbiamo incontrato per chiedergli di aggiornarci sugli sviluppi recenti. «Ci stiamo lavorando proprio in questi giorni», ha esordito con la sua voce pacata, capace però di aprire squarci su scenari inimmaginabili.

Che cos’è cambiato nel nostro modo di vedere il Big Bang?

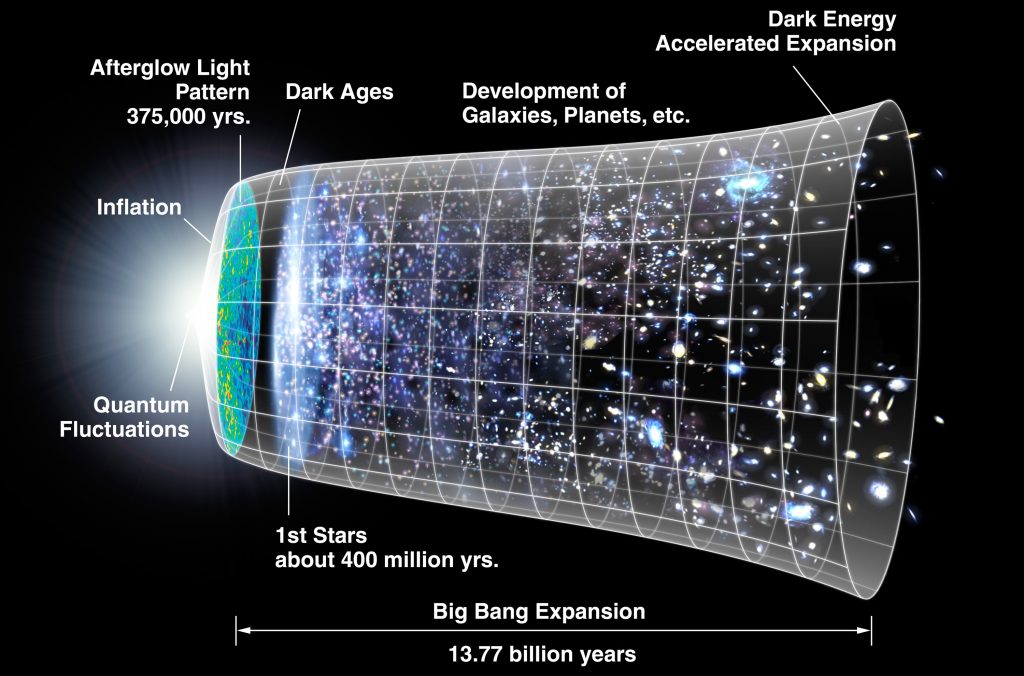
In passato il Big Bang era visto come una singolarità, cioè una situazione di densità e temperatura infinite, che ci impediva di andare al di là nel tempo. Nella nuova visione, il Big Bang è un momento particolarmente interessante della vita dell’universo, ma non è l’inizio e non ha niente di catastrofico: la densità è altissima, ma non è infinita, e la temperatura è altissima, ma non è infinita. L’ordine giusto con cui si sono verificati gli eventi è dunque: prima l’inflazione, poi il Big Bang, e non viceversa come si vede in molte illustrazioni.

Perché c’è bisogno di una fase inflazionaria iniziale per risolvere i problemi della vecchia cosmologia?

La ragione è che, altrimenti, bisognerebbe aggiustare in modo incredibilmente preciso le condizioni in corrispondenza del Big Bang per spiegare l’universo attuale. Ma l’inflazione da sola non basta: un punto su cui insisto da tempo è l’importanza della meccanica quantistica in questa nuova cosmologia. L’inflazione, se non ci fosse la meccanica quantistica, darebbe un universo completamente omogeneo, cioè privo delle strutture su grande scala che ci circondano: galassie, ammassi di galassie, vuoti, filamenti ecc.

Alla luce di queste nuove idee, dunque, il Big Bang non è l’inizio ma un semplice punto di svolta nella storia dell’universo. Come possiamo pensarlo?

È un momento in cui si passa da un’energia potenziale, quella che determina l’inflazione, alla creazione di un gas particelle ad alta temperatura. Per descrivere quello che accade, spesso ricorro all’immagine di una cascata: a monte della cascata c’è molta energia potenziale; ma quando l’acqua scende l’energia potenziale si trasforma in energia cinetica.

Come descriverebbe l’universo prima del Big Bang?

Caratterizzare l’inizio della fase inflazionaria non è facile. Ma nell’ambito delle teorie delle stringhe esiste una possibilità abbastanza motivata di descriverlo sulla base di certe simmetrie che la teoria stessa possiede. La teoria delle stringhe è un completamento della teoria quantistica dei campi (cioè la teoria alla base del Modello Standard delle particelle elementari, ndr) e la modifica quando si considerano scale di lunghezza molto molto piccole…

Piccole rispetto a che cosa?

La scala di riferimento è la cosiddetta lunghezza di stringa. Su scale molto maggiori della lunghezza di stringa vale la teoria quantistica dei campi convenzionale. Però questa scala può evolvere nel tempo.

In che senso, e in che modo, la lunghezza di stringa può cambiare nel tempo?

La lunghezza di stringa è, in realtà, l’unica scala di lunghezze della teoria e possiamo tenerla fissa, come unità di misura di tutte le lunghezze. Quello che cambia è la forza con la quale le stringhe interagiscono. Siccome in teoria delle stringhe le interazioni sono unificate, la forza di gravità, la forza elettromagnetica e le forze nucleari forte e debole sono determinate da un’unica costante. Questa costante però è dinamica, cioè è associata a una particella, o se vogliamo a un campo (nella teoria quantistica dei campi, a ogni particella corrisponde un campo e viceversa, ndr), una specie di bosone/campo di Higgs: si chiama dilatone.

Quanto più piccola è la forza, in particolare quella di gravità, tanto più grande è il rapporto tra la scala della stringa e la scala di Planck (che è legata alla costante di Newton e vale 10^-35 m). Quindi, se si fissa una delle due scale di lunghezza, l’altra dipende dal valore del campo del dilatone e dunque può cambiare nel tempo.

Torniamo alla domanda iniziale: come era, allora, l’universo prima dell’inflazione?

Il vecchio modello di cosmologia su cui ho lavorato con Maurizio Gasperini (Università di Bari) e con altri collaboratori parte dall’ipotesi che l’universo inizi con interazioni debolissime. In questo regime è facile risolvere le equazioni della teoria delle stringhe, perché si parte da costante di accoppiamento molto piccola e da una curvatura molto piccola dello spazio-tempo. Poi la costante di accoppiamento e la curvatura evolvono e prendono valori sempre più grandi, finché si arriva alla scala di curvatura della stringa stessa, cioè quando il raggio di curvatura dell’universo è dell’ordine della lunghezza di stringa. A quel punto, la costante di accoppiamento arriva ai valori attuali e avviene questa transizione che noi associavamo al Big Bang. Si chiamava modello di pre-Big Bang, perché descriveva questa fase precedente, che tecnicamente parlando era anch’essa inflazionaria, cioè aveva caratteristiche simili a quelle dell’inflazione più convenzionale.

Alla fine, si può dire che è il dilatone che spinge l’espansione dello spazio durante l’inflazione?

Esattamente. Le equazioni di Friedman, che descrivono l’espansione dell’universo, ci dicono che la velocità dell’espansione è data dal prodotto della costante di Newton per la densità. Nel nostro scenario, durante la fase che precede il Big Bang, cresce sia la costante di Newton sia la densità; quindi l’espansione è di tipo accelerato, sinonimo di inflazione.

E se ne esce con una transizione di fase, il Big Bang.

Sì, e qui veniamo alle novità. Negli ultimi anni alcuni studi, in particolare di Olaf Hohm e Barton Zwiebach, sono riusciti a tener conto in modo completo delle simmetrie che caratterizzano questa fase di pre-Big Bang. Noi l’avevamo fatto solo nel regime in cui le curvature sono piccole e l’accoppiamento è piccolo. Usando questi nuovi risultati, con Maurizio Gasperini siamo riusciti a vedere che si può effettivamente avere una transizione che connette le due fasi, pre e post Big Bang, attraverso un rimbalzo. Invece di Big Bang preferiamo quindi chiamarlo Big Bounce (“Grande Rimbalzo”). Fino a poco tempo fa non c’erano tecniche matematiche per descriverlo in dettaglio, ma grazie a questo sviluppo teorico siamo riusciti a costruire delle soluzioni perfettamente regolari. Uno degli ostacoli che avevamo sembrerebbe risolto.

Che cosa succede al dilatone durante il Big Bounce?

Finché siamo nel regime di interazioni molto deboli, il dilatone si comporta come una particella senza massa. Quando invece si entra in un regime simile a quello attuale, il dilatone si può stabilizzare, un po’ come fa il campo di Higgs nella transizione elettrodebole.

Però, quando dà la massa alle particelle, il bosone di Higgs condensa. Anche il dilatone condensa?

Esattamente, dato che si stabilizza prendendo un valore non nullo. Quando condensa al minimo del suo potenziale, il dilatone fornisce il valore di tutte le forze. Come il campo di Higgs dà massa alle particelle del Modello Standard, così il dilatone dovrebbe dare la forza delle loro mutue interazioni. Per esempio, dovrebbe dirci quanto vale la costante di Newton e quanto è grande la costante di struttura fine (che vale circa 1/137, ndr). La teoria delle stringhe, se un giorno sarà risolta, dovrebbe fornire quel numerino come conseguenza del valore attuale del campo del dilatone.

E, condensando, il dilatone genera il Big Bang, giusto?

Genera la transizione tra la fase inflazionaria e il Big Bang inteso come reheating. È il “rimbalzo”, il rebound.

Dopo il Big Bang, però, che cosa succede al dilatone? Rimane fisso, invariato nel tempo?

Questa è una domanda molto interessante, perché in effetti sembrerebbe quasi un miracolo che se ne stesse lì tranquillo e non si muovesse più. Però, se avesse un’evoluzione anche piccola nel tempo, vorrebbe dire che certe costanti della natura dipenderebbero dal tempo. E ci sono molti esperimenti che fanno vedere che invece, nel nostro passato, anche remoto, varie costanti fisiche sono rimaste invariate. Quindi ci sono alcuni limiti su quale possa essere stata l’evoluzione del dilatone dopo il Big Bang. Se invece si osservassero piccole variazioni della costante di struttura fine nel tempo, o anche piccole deviazioni dall’universalità della caduta libera – fenomeni sotto attento scrutinio sperimentale da vari decenni – questa sarebbe una scoperta molto importante che punterebbe il dito verso la teoria delle stringhe.

Il dilatone potrebbe spiegare anche il mistero dell’energia oscura?

Ha colpito nel segno. In un lavoro con Thibault Damour, un fisico teorico francese che ha contribuito con i suoi calcoli alla rivelazione delle onde gravitazionali, avevamo sviluppato un modellino in cui effettivamente l’energia oscura è legata al dilatone. È un modello un po’ diverso da quello appena descritto: il dilatone, invece di andare a finire a un valore finito e fermarsi lì, continua a evolvere e da valori iniziali molto negativi va a finire a valori molto positivi. Questo limite del dilatone che cresce all’infinito è potenzialmente interessante ed è legato a un’idea di Andrej Sacharov, la cosiddetta induced gravity. L’idea è che si parte da una teoria classica in cui manca il termine usuale che fornisce le equazioni di Einstein. Però gli effetti quantistici inducono la costante di Newton e le equazioni di Einstein. Insomma, è come dire che la gravità è un fenomeno di origine quantistica. Questo limite in cui il dilatone va all’infinito (positivo) è essenzialmente lo stesso concetto. Una volta Sacharov venne al Cern e chiese di vedermi per informarsi sulla teoria delle stringhe. Mi chiese se nella teoria ci fosse una induced gravity. Io, però, a quei tempi non avevo pensato a questa possibilità; quindi gli risposi di no, che mi sembrava che la gravità ci fosse ab initio. E solo vari anni dopo, quando Sacharov era ormai morto, mi accorsi che questo limite concretizza proprio la sua idea.

Nella teoria delle stringhe, tra le particelle ancora da scoprire, c’è solo il dilatone?

No, c’è anche un assione. E ci sono altri campi scalari che tra l’altro, se non condensano, cioè se non si bloccano al minimo di un loro potenziale, possono generare anch’essi variazioni delle costanti naturali.

Torniamo al pre-Big Bang. La teoria delle stringhe dice qualcosa su come potrebbe nascere il tempo?

Su questo ho idee abbastanza convenzionali. So che si parla di un tempo che scaturisce in modo emergente, io la vedo un po’ diversamente. La teoria in genere parte dalle coordinate delle stringhe, temporali e spaziali. C’è la coordinata della stringa che si muove nel tempo e descrive una superficie. Quello che ho potuto vedere, in alcuni studi, è che – proprio perché la stringa ha dimensioni finite – non è possibile misurare distanze spaziali e forse anche intervalli temporali che siano più piccoli di questa scala. Con alcuni collaboratori, abbiamo introdotto un Principio di Indeterminazione Generalizzato (GUP), che aggiunge al Principio di Indeterminazione di Heisenberg anche l’impossibilità di misurare distanze troppo piccole. Quindi il mio punto di vista è che, finché non siamo in un regime in cui domina la lunghezza di stringa rispetto ad altre scale, possiamo vivere tranquillamente con i nostri concetti usuali di spazio e di tempo. Però, quando siamo a scale di curvatura e/o di temperatura al di sopra di un certo valore critico, la stringa interviene con il suo nuovo principio di indeterminazione e fa sì che non sia più possibile misurare intervalli di spazio e di tempo più piccoli di quella scala. È come se lo spazio-tempo diventasse discreto: solo incrementi discreti sono possibili. È una specie di quantizzazione dello spazio e del tempo. In altre parole, in quelle condizioni lo spazio-tempo continuo non è una buona descrizione della natura.

Quindi non c’è stato un inizio del tempo?

Non ci sarebbe stato un inizio. Il fatto di partire da uno spazio-tempo piatto, con costante di accoppiamento piccola, risolve anche un problema noto come problema trans-Planckiano, cioè il fatto che quando si va indietro nel tempo, se si riporta per esempio la scala di una galassia all’inizio dell’inflazione, questa diventa una scala sub-Planckiana (cioè inferiore alla lunghezza di Planck, che è la lunghezza minima concepibile in natura, ndr). Ma questo è un problema: come si fa a descrivere questo inizio? Ecco, questo tipo di problemi non esiste nel nostro modello, proprio per il fatto che la fase iniziale nel nostro scenario non è affatto sub-Planckiana.

Però questo vuol dire che prima potrebbe esserci stata qualsiasi cosa, andando indietro all’infinito nel tempo.

Sì, certo.

Continua a essere spostato all’indietro nel tempo il problema dell’origine di tutto.

Sì, questo è vero.

E allora non sono vere e proprie condizioni iniziali.

Sì, diciamo che è modello basato sull’assunzione che l’universo sia iniziato nel modo più semplice possibile, cioè molto piatto e con interazioni debolissime. È un postulato che con Alessandra Buonanno e Thibault Damour abbiamo chiamato “ipotesi di un passato asintotico banale” (Asymptotic Past Triviality).

E in quelle circostanze l’entropia era bassa?

Sì, l’entropia era molto bassa. Si può vedere facilmente come l’entropia venga generata di nuovo tramite la creazione di particelle. L’universo diventa sempre più curvo, crea particelle e al Big Bounce è caldo.

Però, se nasce con entropia bassa, non è un universo improbabile?

Effettivamente, se vogliamo sì. Quello che mi piace è che nel momento del bounce si vede che si satura un certo limite teorico sull’entropia. Ci sono varie proposte in fisica sui limiti massimi dell’entropia (limite di Bekenstein, limite olografico ecc.) e la cosa interessante è che all’inizio l’entropia era molto bassa. In un certo senso è una tautologia: siccome l’entropia aumenta, all’inizio deve esser bassa. Ma, al momento del bounce, o del Big Bang, l’entropia sembra massimizzare questi limiti. Allora si potrebbe pensare: ma se l’entropia è già massimizzata, come faccio ad andare avanti? La novità è che questi limiti sull’entropia non sono fissati una volta per tutto, ma sono legati alla geometria dello spazio-tempo: corrispondono ad avere un certo numero di gradi di libertà, cioè di entropia, per ciascun volume di Hubble, che corrisponde essenzialmente alla porzione osservabile dell’universo a un dato istante. Allora, quando l’universo si espande e diventa sempre meno curvo, il volume di Hubble aumenta e aumenta anche il limite superiore accettabile per l’entropia. Quindi si parte al Big Bounce da uno stato massimamente entropico, però l’evoluzione dell’universo fa sì che sia possibile aumentare ulteriormente l’entropia, perché aumenta il limite. Tanto è vero che oggigiorno siamo molto lontani dal saturare questo limite. Però, ripeto, al bounce il limite sarebbe già stato raggiunto, e in un certo senso il bounce avviene perché, se non avvenisse, si andrebbe al di là del limite massimo consentito.

Tornando al nostro universo, resta una questione: che cosa c’è oltre l’orizzonte visibile?

Normalmente ci si aspetterebbe che l’universo fosse molto più grande di quello che osserviamo. Nel nostro scenario dipende molto da che cosa è successo durante la fase iniziale. Con Damour avevamo avanzato l’idea che questa fase iniziale assomigliasse al collasso gravitazionale di un buco nero, e che l’universo che emerge da questa fase possa essere molto più grande dell’universo osservabile. In questo schema, ci potrebbero essere molti universi paralleli, tutti sconnessi tra loro da un punto di vista spazio-temporale, nel senso che sarebbe impossibile entrare in comunicazione con loro.

I vari universi sarebbero tutti come il nostro, o potrebbero avere caratteristiche diverse?

Potrebbero anche avere leggi della fisica diverse. Nello scenario che abbiamo sviluppato alla fine degli anni ’90, c’è uno stato iniziale che descriviamo come un mare caotico di onde dilatoniche e gravitazionali. Questo stato iniziale tende a evolversi verso la formazione di buchi neri; ma questo può avvenire in punti e in momenti diversi. All’interno dell’orizzonte di ciascun buco nero può avvenire un Big Bounce e nascere un universo. Qui giocherebbe un principio antropico: noi esistiamo in uno di questi possibili universi che ha certe caratteristiche adatte a generare al suo interno la vita e gli esseri umani. Poi magari al di là, ma molto molto lontano da noi, in luoghi disconnessi, potrebbero esistere altri universi, altre dimensioni… nella teoria delle stringhe ci sono anche tutte le dimensioni nascoste. Anche quelle possono cambiare, perché ci sono varie configurazioni in cui possono trovarsi.

Che relazione c’è tra quei buchi neri primordiali e quelli che conosciamo?

All’interno di ogni universo si possono formare buchi neri astrofisici, di tipo più convenzionale. Ma anche all’interno di un buco nero astrofisico ci sarebbe, secondo la teoria di Einstein, una singolarità simile a un Big Crunch (un “Grande Collasso”). Cosa ne è di questa singolarità se si sostituisce la teoria di Einstein con quella delle stringhe? Questa è una domanda affascinante ancora senza risposta.

Come si può trovare una controprova sperimentale di queste idee?

Per esempio, attraverso la radiazione cosmica di fondo. Il nostro vecchio modello pre-Big Bang ha uno spettro di perturbazioni gravitazionali blu, cioè spostato verso le alte frequenze, e ci aspettiamo poca polarizzazione della radiazione di fondo. La polarizzazione di tipo B, che si sta cercando come prova dell’inflazione, in questo scenario sarebbe inosservabile. Negli studi più recenti, però, sembra esserci la possibilità di usare la teoria delle stringhe per innescare un’inflazione più convenzionale, in cui la polarizzazione sarebbe abbastanza grande da essere misurabile.

Questo scenario che abbiamo esaminato è l’unico possibile nella teoria delle stringhe?

Ci possono essere anche altri scenari. Quello di cui abbiamo parlato, e che ho studiato per molti anni, non è l’unico modello, ma direi che è il più semplice. Estrae solo le informazioni dovute a queste nuove simmetrie per dire: se c’è questa soluzione dopo il Big Bang (cioè l’universo che conosciamo), ce ne dovrebbe essere una duale nella fase antecedente. La simmetria trasforma una soluzione nell’altra, e in entrambe il dilatone svolge un ruolo centrale. Se il dilatone è costante oggi, non poteva essere costante prima. Questo è intrinseco in questa simmetria. Sono due fisiche diverse ma connesse dal fatto che c’è una simmetria nelle equazioni.

Ci sono però anche modelli ciclici, come quello sostenuto dal premio Nobel Roger Penrose o come quelli detti dell’universo ecpirotico. Ci sono tante idee in giro e probabilmente risulteranno tutte sbagliate via via che si progredisce sia sul lato teorico sia su quello sperimentale. Però ci sono anche questi concetti più generali per i quali sono pronto a mettere la mano sul fuoco: bisogna scordarsi l’idea del vecchio Big Bang, perché confonde solo le idee. Quello che noi osserviamo oggigiorno, per esempio nella radiazione fossile di fondo, non ha nulla a che vedere con l’inizio dell’universo. Ha a che vedere, invece, con la fine dell’inflazione.

Link e approfondimenti

• Un articolo sulle origini della teoria delle stringhe sul Cern Courier (in inglese).
• Un video che spiega la teoria delle stringhe (in inglese).
• La storia dell’universo in un multimedia di Focus, a cura di Andrea Parlangeli. E il dossier di copertina di Focus n° 377.