Negli anni ’70, nel suo libro On Numbers and Games, il matematico John Horton Conway (1937-2020) presentò al mondo una nuova classe di numeri, i surreali, da lui inventati e battezzati così dall’informatico Donald Knuth. Il libro di Conway è noto attraverso l’acronimo ONAG, che in ebraico vuol dire piacere spirituale (עֹנֶג). Conway è stato uno dei matematici contemporanei più originali e profondi. Si è occupato di teoria dei gruppi, dei giochi, dei numeri, dei nodi. È stato un matematico eclettico, brillante e arguto, che non ha disdegnato mai nessun problema come poco nobile, nemmeno se originava dalla matematica ricreativa. A lui si deve anche un modello universale di calcolo, noto come gioco della vita, di cui abbiamo già parlato su Josway. Per dare un esempio della sua versatilità, ricordiamo che ha inventato un algoritmo di calcolo mentale per risalire da una data qualsiasi al giorno della settimana che le corrisponde (basato sul fatto che alcune date facili da ricordare come il 4/4, 6/6, 8/8, 10/10, 12/12 e anche il 25 aprile cadono tutte nello stesso giorno della settimana, il doomsday). Tristemente, Conway è morto di Covid-19.
Numeri, nel senso più generale possibile
Per sgomberare il campo da questioni tecniche dichiaro subito che i numeri surreali sono la più grande classe possibile di numeri, nell’universo degli insiemi, che estende tutte le classi di cui abbiamo parlato finora (v. articolo precedente), compresi gli infiniti e gli infinitesimi, ad esclusione degli immaginari e dei quaternioni, che però si possono aggiungere senza difficoltà. E, come dicono i logici, queste estensioni sono conservative ovvero si possono definire sui surreali operazioni di somma, differenza, prodotto, divisione, esponente, logaritmo, e quant’altro si può esprimere “ragionevolmente” sui numeri reali, in modo da conservare il valore che queste operazioni avrebbero se ristrette ai loro domini originali. Per esempio, la somma di due interi visti come surreali è il surreale corrispondente alla somma dei due interi, oppure il surreale corrispondente al quadrato del surreale corrispondente a π è il surreale corrispondente a π². Quindi abbiamo a disposizione tutti i numeri di cui disponevamo prima con tutte le loro proprietà, tra i surreali, ma possiamo dare senso in modo coerente a nuovi oggetti come l’infinitesimo 1/ω, oppure ad apparenti eccentricità numeriche come √(ω+1) + π/ω².
La risposta finale
Dunque i numeri surreali danno, forse, la risposta a finale alla nostra domanda fondamentale, da cui eravamo partiti: che cos’è un numero?
Un numero è un gioco
I numeri surreali sono giochi. Ovviamente, sono giochi un po’ più stilizzati degli scacchi, del bridge, di Monopoly o di Carcassonne. L’ambientazione non ha importanza. I giochi in questione sono una versione astratta dei giochi deterministici a due persone con informazione perfetta. A informazione perfetta vuol dire che l’avversario è a conoscenza delle nostre possibili mosse. Si possono descrivere, come nella rappresentazione insiemistica dei numeri reali, da una coppia di insiemi: l’insieme S delle mosse ammesse per una giocatrice a sinistra e l’insieme D delle mosse ammesse per una giocatrice a destra. In ossequio a Conway, indicheremo tale coppia con {S|D}. A ogni turno, ogni giocatrice sceglie una mossa nell’insieme delle mosse che le competono, se questo non è vuoto. Se l’insieme di mosse a sua disposizione a un certo punto è vuoto, allora perde e l’altra giocatrice vince. Ma quali sono le mosse di questi giochi? Ecco uno dei colpi di genio di Conway: le mosse stesse dei giochi di Conway sono giochi, e precisamente quelli che si vengono a determinare una volta fatta quella mossa.
I numeri, nel senso più ampio del termine, sono giochi… Dei quali, a sua volta, ogni mossa è un gioco
Costruiti sul vuoto
Quindi, in analogia a quanto accadeva con gli insiemi, tutto l’universo dei giochi è fatto a partire da giochi le cui mosse sono giochi, le cui mosse sono giochi, e così via… E come con gli insiemi anche con i giochi, prima ancora di sapere che cos’è un gioco ne abbiamo già uno, quello vuoto. In questo gioco perde chi gioca per primo, vince chi gioca per secondo. E ancora, esattamente come per gli insiemi, anche per i giochi avviene che tutti i giochi sono costruiti a partire dal gioco vuoto. Tutti i giochi di Conway terminano quindi con la vittoria di una delle due giocatrici, perché prima o poi tutte le catene di mosse terminano sul gioco vuoto. Quindi, tali giochi hanno necessariamente una strategia vincente per una qualche giocatrice: se non ci fosse una strategia vincente, ogni giocatrice potrebbe sempre giocare quella mossa per la quale l’avversaria non ha una mossa vincente, e il gioco non terminerebbe mai.
Come con gli insiemi, anche i giochi si possono costruire a partire dal gioco vuoto
Strategie vincenti
Nell’universo di Conway ogni numero si può giocare. Se questo numero è uguale a 0, allora c’è una strategia vincente per la prima giocatrice (che può essere a destra o a sinistra), altrimenti per la seconda. E se questo numero è strettamente positivo c’è una strategia vincente per la giocatrice sinistra; se invece è strettamente negativo ce n’è una per la giocatrice destra.
Un esempio cinematografico
Come iniziazione ai giochi di Conway, si può partire dal celebre gioco del Nim che veniva giocato per ingannare il tempo nella città termale de L’anno scorso a Marienbad (L’Année dernière à Marienbad), il film diretto da Alain Resnais e sceneggiato dallo scrittore Alain Robbe-Grillet, che vinse il Leone d’oro a Venezia nel 1961.
Con i fiammiferi
Il gioco del Nim è il seguente. Si dispongono delle righe di fiammiferi in parallelo, come avviene nel film. Quando è il proprio turno, una giocatrice toglie alcuni fiammiferi, anche tutti, ma da una riga soltanto. Vince chi non lascia più nessun fiammifero sulla tavola. (Veramente nel film si gioca la variante misère del gioco, ovvero quella nella quale perde chi prende l’ultimo fiammifero, che richiede un’analisi leggermente più complicata). La classica distribuzione di partenza ha 4 righe di 1,3,5 e 7 fiammiferi rispettivamente. La rappresentazione di Conway della configurazione iniziale del gioco del film è data da 1*+3*+5*+7*.
Quasi come numeri
Ovvero il gioco è espresso come la somma di 4 giochi, ciascuno corrisponde ad una riga. I numeri asteriscati sono i giochi:
0*={|}
1*={0*|0*}
2*={0*,1*|0*,1*}
3*={0*,1*,2*|0*,1*,2*}
4*={0*,1*,2*,3*|0*,1*,2*,3*}
…
Attenzione, questi non sono ancora i numeri surreali. In realtà, si tratta di numeri non in senso tradizionale (per questo di usano gli asterischi * per indicarli), in quanto non si sommano tra loro con le regole dei numeri naturali. Li chiameremo numeri star (*).
Dal gioco alla somma
Come ci si può facilmente vedere, in ciascuno di questi giochi corrispondenti ai numeri star le mosse per la giocatrice sinistra sono uguali a quelle della giocatrice destra. Facendo una mossa la giocatrice trasforma una riga in una riga più breve. Ovvero trasforma uno degli addendi del gioco somma in un altro. E come si definisce un gioco somma di due giochi G₁={S₁|D₁} e G₂={S₂|D₂}?
Il gioco somma G₁+G₂ ha una formula un po’ più complicata della somma diretta delle mosse. Nel caso del Nim, infatti, fatta una mossa ci si trova nel gioco ottenuto come somma delle righe intonse più quello della riga nella quale è stata trasformata la riga sulla quale si è intervenuti. Traducendo in formule, si ha:
G₁+G₂={s₁ + G₂, G₁ + s₂ | d₁ + G₂, G₁ + d₂} per tutti gli s₁∈S₁, s₂∈S₂, d₁∈D₁, d₂∈D₂
A somma zero
Questa somma si può calcolare esplicitamente, e nel nostro caso fornisce 1*+3*+5*+7*=0. Quindi c’è una strategia vincente per la seconda giocatrice, come è ben illustrato nel film.
L’idea di Conway
Tutto questo serve a dare un’idea dell’idea di Conway: ogni numero corrisponde a un gioco, i giochi possono essere composti e decomposti in modo da ottenere altri giochi, ovvero altri numeri, e se calcoliamo questi numeri opportunamente possiamo sapere se i giochi sono vincenti per la prima oppure per la seconda giocatrice.
Dai giochi ai numeri surreali
Quelli usati nel Nim sono giochi imparziali, come li chiama Conway, ovvero le mosse della giocatrice sinistra e quelle della giocatrice di destra sono uguali. Ci siamo serviti di questo esempio solo a scopo introduttivo. I numeri surreali, invece, nascono quando ciò non accade. In realtà non tutti i giochi di Conway corrispondono a numeri surreali, ma solamente quelli per i quali ogni mossa per la giocatrice di sinistra è minore di quelle della giocatrice di destra. Non entriamo qui nella definizione di minore, perché è un po’ uno scioglilingua. Basta saperlo, e basta sapere che la regola della somma è sempre la stessa che abbiamo già dato e che vale giù in generale per tutti i giochi.
Trattini e alberelli
Arriviamo ora ai numeri surreali. Per raffigurarli, è utile fare riferimento a un altro gioco inventato sempre da Conway, il gioco di Hackenbush, che è una generalizzazione di quello del Nim. In figura è presente una possibile configurazione iniziale.
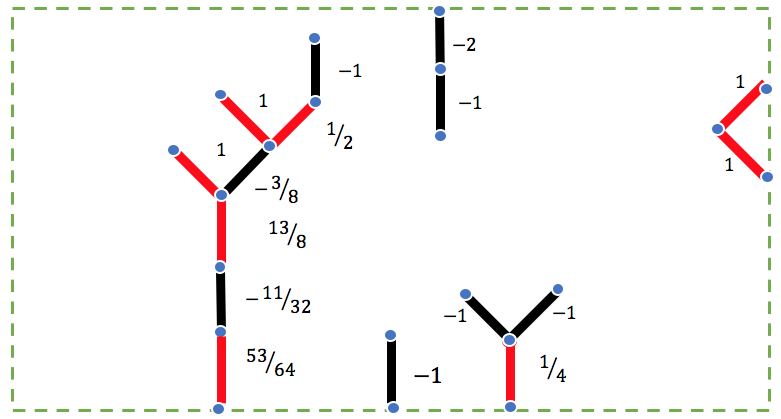Ogni alberello bicolore è ancorato al bordo tratteggiato. A ogni mossa la giocatrice rossa, quella di sinistra, può togliere un trattino rosso e quella nera, di destra, un trattino nero. Perde chi non ha più trattini del proprio colore da togliere. Attenzione però, se si toglie un trattino si rimuovono anche tutti quelli che rimanevano ancorati al bordo tratteggiato grazie a quel trattino. Chi ha una strategia vincente nella configurazione iniziale del disegno? Accanto a ogni trattino compare un numero. Questo è il numero surreale che corrisponde al valore di quella mossa. Come si calcolano questi numeri è un po’ laborioso. Cerchiamo di darne un’idea.
Il significato dello 0
Questo gioco corrisponde a {|}=0, ovvero né la giocatrice rossa né quella nera possono muovere, vince chi va per secondo;
Il significato dell’1
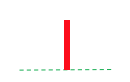Questo gioco corrisponde a {0|}=1 ovvero la giocatrice rossa può fare una mossa la nera no; vince la rossa sia che vada per prima che per seconda;
Il significato del -1
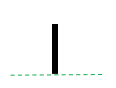Questo gioco corrisponde a {|0}=-1 ovvero la giocatrice nera può fare una mossa la rossa no; vince la nera sia che vada per prima che per seconda;
Il significato di 1/2
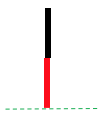Questo gioco corrisponde a {0|1}=1/2 ovvero la giocatrice nera può fare una mossa che ne lascia una alla rossa mentre la rossa ne può fare una che non ne lascia alla nera. Vince la rossa sia che vada per prima che per seconda.
Il significato di 3/4
Corrisponde a {1/2 |1}=3/4 ovvero la giocatrice nera può lasciare il gioco 1 mentre la giocatrice rossa può lasciare la nera senza mosse oppure una situazione 1/2. Vince di nuovo la rossa sia che vada per prima che per seconda.
Come ritrovare gli altri numeri
Possiamo così, più in generale, trovare i numeri naturali 1={0|}, 2={1|}, 3={2|}… Poi i numeri negativi -1={|0}, -2={|-1}, -3={|-2}… E i razionali 1/2={0|1}, 1/4={0|1/2}, 3/4={1/2|1}…
Come calcolare il disegno generale? Il valore del gioco costituito da più alberelli attaccati al bordo è la somma algebrica dei valori di ogni singolo alberello. Il modo di calcolare il valore di ogni singolo alberello è più laborioso. Gli esempi elementari dati possono però essere sufficienti a darne un’idea. Comunque il valore del disegno in figura è 5/64, dunque vincono i rossi.
Dall’infinitesimo all’infinito
Ci sarebbe ancora moltissimo da dire sui numeri surreali, ma mi costringerebbe a riscrivere i primi capitoli di ONAG, e non vorrei incorrere nel plagio. Mi limito pertanto a dare la rappresentazione del più semplice gioco infinito ω={0,1,2,…,n,…|} nonché del suo successore ω+1={0,1,2,…,n,…,ω|} e predecessore ω-1={0,1,2,…,n,…|ω}. Concludo quindi consapevole di aver fatto vedere solo una parte così piccola dell’universo surreale, che la definirei con il gioco {0|1, 1/2, 1/4, 1/8, 1/16…}.
Indovinate chi è? È il gioco infinitesimo.
