Un funambolo in equilibrio su una corda infuocata nel centro di Castel del Monte conclude il film di Matteo Garrone Il racconto dei racconti (2015) tratto dalle fiabe seicentesche de Lu cunto de li cunti. L’iterazione nel titolo amplifica la narrazione. Il funambolo ha percorso una diagonale dell’ottagono che delimita il cortile del castello, quello che secondo alcuni era una enorme vasca. Nella visione prospettica l’ottagono ci appare regolare, in realtà non lo è, ma quel che vediamo condiziona quel che immaginiamo e allora concediamoci l’approssimazione.
Ottagono nell’ottagono
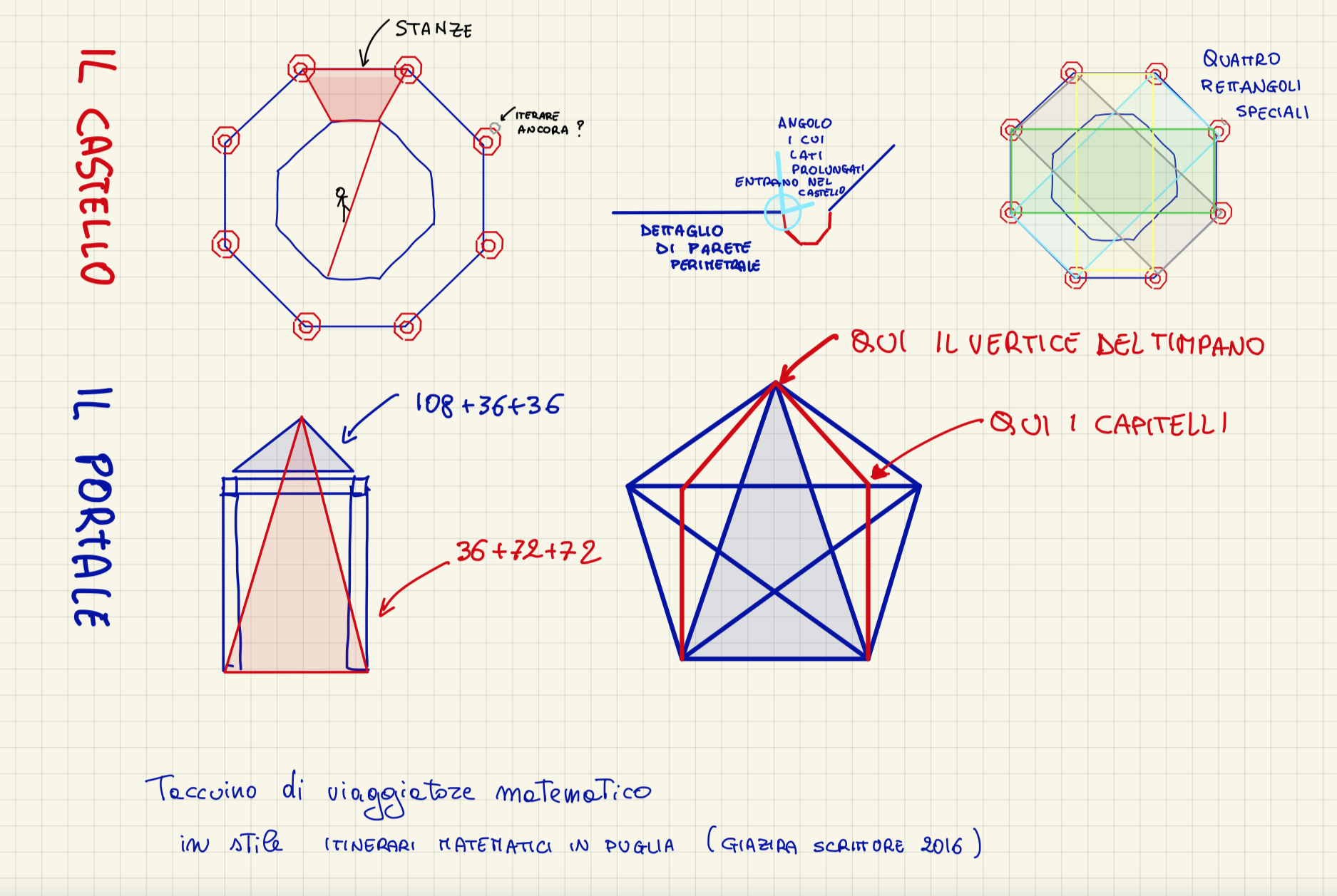
Disegniamo questa forma su un foglio e chiediamoci: come costruiremmo attorno a siffatto vuoto un castello? Come in certe cornicette che facevamo da bambini sulla prima pagina del quaderno, ci risulterà naturale tracciare un altro ottagono regolare di stesso centro intrappolando la vita del castello tra questi due poligoni, in un rincorrersi di stanza in stanza. Le stanze si ottengono congiungendo i vertici omologhi dei due ottagoni e sono quindi tutte trapezoidali, anche la sala del trono.

Come una corona
Se il cortile fosse stato circolare, questo gioco ci avrebbe condotti a una corona circolare, invece con l’ottagono si ha solo una corona. Già, quella del Sacro Romano Impero con cui Federico II era stato incoronato era appunto ottagonale. Il castello ripete la forma: la corona dell’incoronato. L’iterazione della struttura amplifica il significato. Rispetto al nostro spoglio disegno, la corona era ricca di pietre e perle e immagini. Come adornare allora un castello che abbia la forma di una corona, in modo che moltiplichi l’idea di potenza del suo committente? Moltiplicando le corone.
Numeri e destino
A ogni vertice dell’ottagono mettiamo una torre ottagonale con un vuoto centrale ancora una volta ottagonale. Dall’alto vediamo dunque nove corone ottogonali e 18 ottagoni, mentre percorrendo il perimetro del castello contiamo 56 lati, poiché ciascun ottagono esterno ha ceduto due dei suoi alla corona centrale.
Federico II avrebbe compiuto 56 anni 13 giorni dopo la sua morte, 13 è il giorno di dicembre in cui si spense e 13 sono le monofore che danno sul cortile del secondo piano di Castel del Monte. Si è sempre funamboli su una corda infuocata quando si scrive dello Stupor Mundi e di questo castello, basta pochissimo per bruciare la grande curiosità di chi guarda in un rivolo di coincidenze numeriche e leggende.
La geometria di Castel del Monte è invece una irripetibile ma semplice bellezza.
Reiterando, all’infinito
Lasciamo i numeri e torniamo al nostro disegno. All’esterno abbiamo un poligono non convesso. Vi sono 16 vertici i cui ideali prolungamenti dei lati entrano nel castello. Sugli altri vertici un appassionato di frattali può immaginare di mettere altre corone ottogonali più piccole e iterare questo processo all’infinito.
Se a ogni passo manteniamo lo stesso rapporto che i mastri dell’imperatore usarono nel milleduecento per costruire le torri esterne, dalla teoria delle serie geometriche sappiamo che la nostra ideale costruzione non andrà molto lontano dalla collina di Andria.
Stelle e castelli
La posizione del castello è forse la sola certezza da cui partire per capire il ruolo del maniero nella rete federiciana di strutture che controllavano il territorio sia per ragioni militari che amministrative. C’è una costellazione di castelli, e come per le stelle è affascinante studiare il grafo che esse formano. Castel del Monte non è un nodo isolato, era funzionale alle comunicazioni con gli altri castelli della Murgia e con il mare.
A proposito di stelle, molto si è scritto sull’effettivo legame tra questo castello e le stelle, fino a ipotizzarlo esclusivamente come osservatorio astronomico.
Il primo scienziato
Ripetizione di castelli, ripetizione di equinozi e solstizi e segni zodiacali da osservare nelle sere d’estate. Ci piacciono i racconti e non parteggiamo per l’una o per l’altra ipotesi sul perché il castello del centesimo di euro avesse quella forma, anzi tifiamo che tutte le ipotesi siano un po’ vere. Possiamo dire con Pietro Greco che Federico II è stato il primo scienziato naturale, ovvero simile a un moderno ricercatore, e la principale intuizione della sua scienza era nella contaminazione delle discipline.

Rapporto aureo
Questo castello, che dal 1996 è iscritto nelle liste dei Patrimoni dell’Umanità dell’Unesco, potrebbe aver ospitato la scrittura delle innovative pagine federiciane sulla caccia al falco. E come per i ricercatori moderni, la matematica era nel cuore del poliedrico imperatore. Egli era il protettore di Fibonacci, che a lui aveva dedicato il Liber quadratorum. Quanto c’è di Fibonacci a Castel del Monte? Più della formula, la forma. Il turista matematico non caschi nella trappola di cercare i primi termini della ben nota sequenza del matematico pisano nel castello. Sì. ci sono 3 scale e 5 camini, 8 stanze e 13 monofore, 21 modiglioni e 34 quadrifogli; ma ci sono anche 10 trifogli e 44 gradini. Concentriamoci piuttosto nel cercare il limite del tasso di crescita della sequenza del pisano: il numero aureo. Di certo chi ha costruito il castello conosceva bene o l’equazione x (x-1) = 1, o la sua visione geometrica “il tutto sta alla parte come la parte alla parte rimanente”. Sono infatti in buona approssimazione di rapporto aureo il lato maggiore e il lato minore delle sale trapezoidali, i lati dei rettangoli ottenuti congiungendo tra loro i vertici opposti tra i 16 di cui parlavamo sopra.
Tripudio di triangoli
Ma il vero capolavoro geometrico del castello è il portale di ingresso. Un triangolo aureo (di angoli 36°, 72°, 72°) si forma tra base e vertice del timpano. Usando questi tre punti, molti hanno costruito il pentagramma stellato che abbia i lati del triangolo come diagonali e “scoperto” molte proprietà del portale.
Un triangolo aureo.
In realtà l’armonia che cogliamo è dovuta alla giusta altezza dei capitelli che poggiano sulla diagonale del pentagramma parallela alla base. Le restanti proprietà sono il giusto dono della geometria alla scelta di avere come timpano uno gnomone aureo (cioè un triangolo di angoli 108°, 36°, 36°). Quando si manda la bisettrice a un angolo di base di un triangolo aureo, si ottengono un nuovo triangolo aureo e uno gnomone aureo. Quando si disegnano le diagonali in un pentagono regolare si ottiene una stella con interno un pentagono regolare in cui potremmo inserire una stella con dentro un nuovo pentagono. Una ripetizione infinita condita di proporzioni auree che si ritrovano a ogni incrocio di diagonali. Si dirà che anche la stella a sei punte, l’esagramma, ha proprietà di riproposizione della stessa figura: l’esagono interno è formato dalla sovrapposizione di due triangoli equilateri che generano anche sei punte equilatere. Ebbene anche questa figura si trova come residuo di pavimento nel castello. Ognuno di questi poligoni ha una semantica religiosa, di religioni diverse.
Per amor di falco
Ma volendo pensare a una matematica di Castel del Monte è meglio tralasciare ogni semantica e concentrarsi sul gioco di suggestive ripetizioni, un’abbondanza di pattern, una ovvia generazione di figure simili secondo i più sobri geometri euclidei. La differenza tra l’ottagono che si ripete nelle torri e i triangoli aurei che si annidano nel pentagramma stellato sta nel fatto che qui la ripetizione è all’interno della figura stessa, così insieme all’infinita ripetizione ci viene in mente l’idea di infinitesimo. Altri hanno osservato che usando la base del triangolo aureo come lato di un altro triangolo aureo e reiterando il procedimento si hanno punti da cui passa la spirale aurea, percorso prediletto da Folgore Gentile, il falco di Federico II, per andare alle prede senza dover cambiare posizione della testa.
Ecco, ci risiamo. Di nuovo tutto sembra convergere per magia avvicinando la matematica al volere dell’imperatore. Invece è solo convergenza della spirale così ottenuta in un punto nemmeno troppo simmetrico del portale dove accade qualcosa di davvero speciale: spingendo proprio lì, il portone potrebbe aprirsi e lasciarci scoprire un dettaglio di bellezza del castello di cui nessuno ha ancora scritto!
Letture e approfondimenti
• Sandra Lucente, Itinerari Matematici in Puglia, Giazira Scritture (2016).




